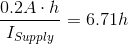Experiment 7: Operational Amplifiers

Introduction:
The purpose of this lab is to condition a signal from a voltage input to a required voltage output.
- Set up voltage divider circuit in order to obtain signal voltage in DC
- Set up Inverting op amp circuit that conditions signal from 0 to 1 v to 0 to -10v
- measure the values
- conclusion

Procedure:
We first consider the entire circuit and determine the necessary resistors
-The sensor may only output a maximum of 1mA of current.

V_cc = 12 V.
V_ee = -12 V. 
V_in = 0 V to +1 V.
V_out = 0 V to -10 V.

We then create a voltage dividing circuit that will condition the input voltage to the specifications of the signal.

R_y = 909 Ohm













potential drop for R_y should now be 1 volt. the pot may be decreased at any point to reduce the voltage.

To be sure, we would like to calculate to make sure R_x will not be over its power limit (1/4 watts).

The minimum resistance that would prevent unnecessary overpowering for R_x is 1152 Ohms, but we will use 1300 ohms as the bare minimum to be safer.











If we were to use the 1300 Ohm resistor, we calculated the value of R_y needed for the potential drop to be 1V.

R_y = 118 Ohm













But the low resistance might condition the OP amp to unappreciably "load" the divider ciruit, so we will use a 10k Ohm R_x value.

These values are what we used for our model.













By decreasing the value of the POT to a value lower than 909, we were able to obtain necessary voltages for the signal input.

Our Circuit and stuff.

More Pictures of the circuit and stuff

The results.

Conclusion:

     The results conclude that there was a gain of -10 through the OP amp, which conditioned the signal to the desired voltage. The current was never over 1 milliamp, and the voltage divider resistor did not burn. The experiment was a success.

Experiment 5: Thevenin Equivalents

Introduction:
     Thevenin Equivalents help us to model linear circuits as a single resistor and power supply. We performed an experiment that proves the validity of Thevenin equivalent circuits.
Objective:
     Test a complicated circuit and measure voltage and current readings through a load, then replace with the thevenin equivalent circuit and measure the voltage and current readings Analyze and interpret the data and perform any error analysis if necessary.

Procedure:
   

This is our original circuit diagram We decided to perform some calculations to find thevenin voltage and resistance.

V1 = V2 = 9V ; Cable 1 (C1) = 100 Ohm ; Cable 2 ((C2) = 39 Ohm ; Cable 3 (C3) = 39 Ohm ; Load 1 (L1) = 680 Ohm ; Potential drop across Load 2 = 8V

Thevenin Voltage = 

Thevenin Resistance / Norton Current

Now that we figured out our thevenin voltage and current, we consider multiple situations for the thevenin circuit.

Required resistance for a potential drop of 8 volts (minimum resistance)

Current through the thevenin equivalent circuit with no load.

Potential drop through load with infinite resistance.

Our Resistors

Setup with resistor boxes

Resistor box and power supply measurements for the thevenin equivalent, theoretical vs actual

Measured voltage vs Theoretical Voltage through the Potentiometer

The results seem to match our predictions on paper within reasonable uncertainty taking into account the differences in our theoretical to actual measurements.

We use the same materials, but with more wires and other necessities for the unthevinized circuit.

Resistor and voltage measurements for our un-thevinized circuit.

The results

The potential drop through the load and also the current matches with our thevenin circuit.


Finally, we will verify that the power supplied is maximized by the formula P = Vth^2/4Rth

Conclusion: The thevenin equivalent allows us to lessen our troubles in calculation when we plug things into a linear ciruit.

Experiment 4: "Transistor Switching"

Introduction

a/b. Use the transistor to switch on and off an LED light, then use your finger.

c. Use a POT to regulate resistance to change the current.

d. Follow up questions.

Procedure

a. Experiment 1: 

The equptments

First Experiment

b. Experiment 2:

The Setup

c. Experiment 3:

Exp 3 circuit

Initial Setup

Experiment and data collection

d. Follow up question:

The Beta gain should be 2.4253.

Experiment 3: "Nodal Analysis"

Introduction
     Perform nodal analysis on a reliable power system.
PART A
     - Find the nodal voltage of point 2 and 3
     - Find the current through battery 1 and 2
     - Calculate power supplied by each battery
     -Perform an experiment to verify the results.
     -Analyze the theoretical with the measured results.
PART B
     - Find the nodal voltages of each node such that the middle two nodes are of equal potential.
     - Find the current through battery 1 and 2
     - Calculate power supplied by each battery
     -Perform an experiment to verify the results.
     -Analyze the theoretical with the measured results.

Procedure

PART A

     This circuit was set up and we calculated the nodal voltage of point 2 and point 3, which turned out to be 10.28V and 8.67V.

We then calculated the current and power associated with the batteries

Our Circuit was set up based on the diagram. Because we used variable box resistors, building the circuit was more complex.

We measured each of the circuit elements taking note of the differences from our theoretical values.

Here is our results.

The measured results were off by a large margin, which was possibly due to the inaccuracy of the meters. It is difficult to measure small currents.

PART B

     The circuit was set up such that point 2 and point three were 9 volts.

The power supply was found to be: and the current also to be:

Power is calculated by this:

We used a variable power supply for this part.

Our measured Voltages and currents were very similar to our predictions.

Conclusion

     Part A: The result wasn't as expected. There were large errors that have to be accounted for, and the measured value of the resistors and voltages compared to the theoretical values aren't the culprit. I believe the power supply was somewhat current dependent or that the current meter couldn't handle precision to the milliamps.

     Part B: When hooked to the variable power supply, the currents and voltages were within the uncertainty of +- 5%, which meant that the circuit was hooked correctly and our theoretical calculations matched our measured values.

Experiment 2: Introduction to Biasing

Introduction

     Determine the resistance required for the LEDs to perform under its maximum load conditions, (biasing).

     Test the circuit and obtain data that either matches or is different from our predictions.

     Calculate efficiency and power.

     

Procedure

     We first calculate by using Ohms law and KVL for the circuit.

Also, R_LED1 = 220 Ohm R_LED2 = 100 Ohm

The designed values of the resistors are not exactly the 

values we need, so we use the values R1 = 220 Ohm and R2 = 470 Ohm.

The final setup of the circuit.

The red and green cables are used to connect the ammeter and potentiometer.

We recorded the data based on these specifications.

The following questions were calculated using the data chart on picture 4 and picture 2.

9V battery is just 0.2A-hr. With both LEDs in the circuit (Fig 2), how long can the circuit

 operate before the battery voltage goes too low?

Calculating the percent error

I_A = I_1 + I_2 (KCL bottom node)

The theoretical value and actual value varied by -17.77%.

Reasoning to this might be that the LED's operating voltage might have been erroneous and that the battery might be current or voltage dependent.

Calculating power efficiency

E = 3.6 / V_B

E = 3.6/9

Power efficiency is calculated to be 41.3%

If the battery is 6V and the current through the LEDs must be specific, then the power efficiency is
1.5 times greater than when the 9V battery was connected.
E = 3.6 / 6

Compared to 9V, the efficiency is increased.

Power efficiency is found to be inversely proportional to voltage, and the maximum efficiency one could get is when the battery gives about 3.6V to the circuit. Any less would mean that the current requirements will be impossible to obtain.

Conclusion.

     The data we have obtained from the circuit matches our theoretical within reasonable uncertainty.
     The circuit is has the most power efficiency when the voltage is at the minimum requirement to sustain the needed current.